LRU 缓存算法

缓存用于存储临时数据，目的是提高数据访问速度，比如 HTTP 缓存可以减少不必要的网络请求；然而，由于缓存的有限容量，当缓存满时，需要选择哪些数据被保留，哪些被替换。这就涉及到缓存置换机制。

LRU(Least recently used: 最近最少使用)算法是一种基于访问历史的置换策略，其核心思想是保留最近被访问过的数据，替换最长时间没有被访问的数据。

原理

下面是 LRU 算法的基本工作原理：

访问记录维护：算法维护一个访问记录表，用于记录每个缓存块被访问的时间信息；
访问时更新：每当某个缓存块被访问时，将该缓存块的访问时间更新为当前时间；
置换选择：当需要置换缓存块时，选择访问时间最久远的缓存块进行替换；

如果有一个大小为 N 的缓存，当第 N+1 个数据需要被缓存时，LRU 算法会选择将最早被访问的那个数据替换出去。

比如下面是一个已经存满数据的缓存（大小为4），A:1代表缓存的 key 是 A，通过这个键可以找到对应的数据1。规定 cache 底部的数据是最近被访问过的，最上面的数据是很早之前被访问过的。

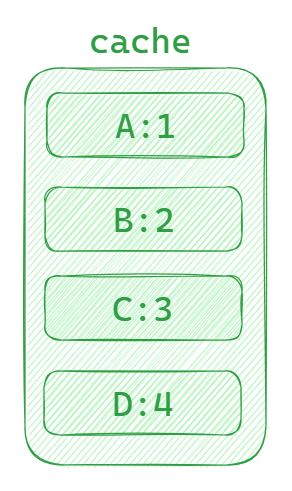
当访问或者修改缓存中的 B 数据时，B 就会是最近一次被访问的，B 将被放到最底部。

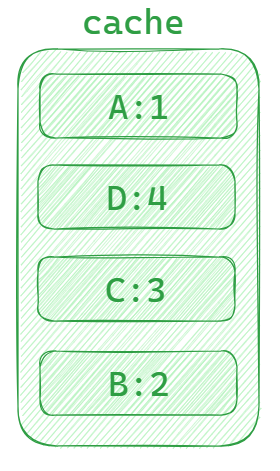
当往缓存中增加新的数据 E:5 时，数据A就会被淘汰（因为它一直没有被再次访问），同时数据E会认为最近被访问，存放到cache的最底部。

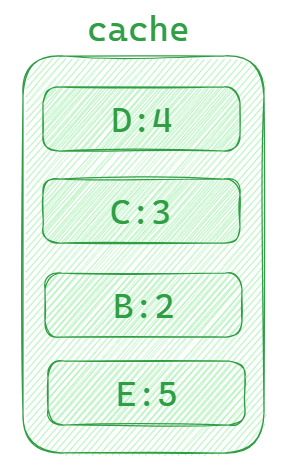
算法实现

LRU算法通常有 put 和 get 操作。

get(key) 从缓存中获取某条数据；
put(key, value) 重新设置或者新增某条数据；

get 和 set 都会触发缓存最近使用时间，更新缓存中的数据顺序

使用数组就可以实现 LRU 算法，思路是：

从缓存中查询数据时，遍历数组，找到对应的 key 和数组索引，使用 splice 把被访问的成员调整到数组末尾；
当 put 的时，先检查是更新还是新增，更新操作与 get 类似。如果是新增还需要检查有没有溢出，如果溢出了需要先淘汰最早被访问的成员（JS 中可以使用数组中的 shift 方法），然后push新数据。

但使用数组实现时间复杂度较高，涉及到遍历操作和数组成员的重新排列（调用 shift 和 splice 时）。如何以 O(1) 的平均时间复杂度实现算法呢？

可以使用 Map + 双向链表 的数据结构实现。

Map 用于增删改查缓存中的数据，它的 value 存的是链表结点，类型为 Map<K, LinkNode<K, V>>。链表结点对应的数据类型为：

/** 链表结点 */
class LinkNode<K, V> {

    /** 上一个结点 */
    public last: LinkNode<K, V> | null;

    /** 下一个结点 */
    public next: LinkNode<K, V> | null;

    constructor(public key: K, public value: V) {}
}

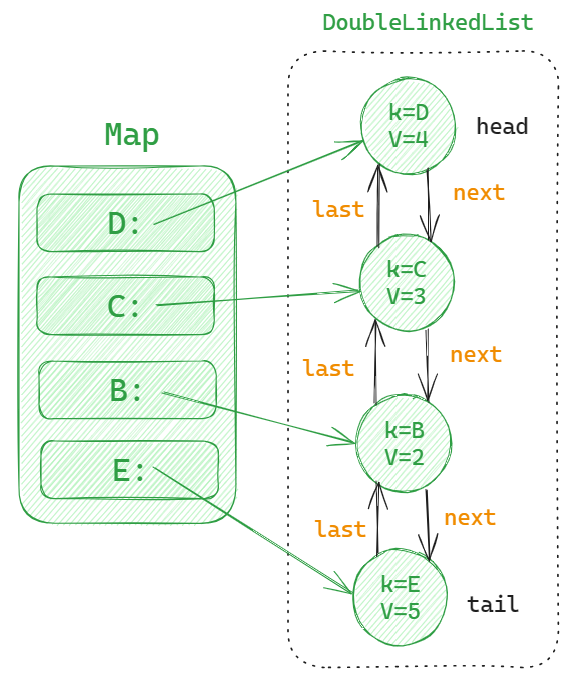
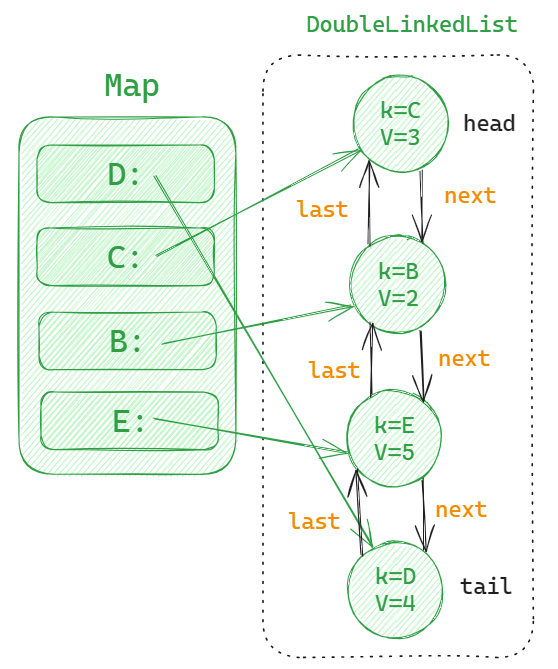
Map+双向链表结构

上图中 E 结点是尾结点，代表最近被访问的数据。D 是头结点，代表最早被访问的数据。

当我们要查询某个数据时，使用 map.get 直接就能查到对应的链表结点。而更新时，可以根据 map.get 找到对应的结点，只需要把这个结点移动到 tail 位置即可，不需要遍历操作。

比如我们访问了 D，那 D 就会是最近被访问的数据，把D对应的结点关联到 tail 位置即可，整个操作过程主要是链表中指针的断开和重建。

Map+双向链表结构

实现双向链表

首先需要定义 head 和 tail 结点。便于操作链表中的其它结点。

class DoubleLinkedList<K, V> {
    /** 链表头部 */
    private head: LinkNode<K, V>;

    /** 链表尾部 */
    private tail: LinkNode<K, V>;
}

然后是往链表中添加新的结点，分两种情况：

是空链表时，即 head=null，直接更新 head 和 tail 的值都是新节点即可；
不是空链表时，需要更新尾结点的指针；

class DoubleLinkedList<K, V> {
    /** 链表头部 */
    private head: LinkNode<K, V> | null = null;

    /** 链表尾部 */
    private tail: LinkNode<K, V> | null = null;

    /** 添加新的结点 */
    public addNode(newNode: LinkNode<K, V>) {
        // 如果没有头结点，说明是个空链表
        if (!this.head) {
            this.head = newNode;
            this.tail = newNode;
        } else {
            // 有头节点时，把新结点添加到链表尾部
            this.tail.next = newNode;
            newNode.last = this.tail;
            this.tail = newNode;
        }
    }
}

接着是把某个结点移动到链表尾部，过程是把该结点的前后结点相连，然后再把这个结点添加到尾部。这个操作用于更新“最近使用的数据”。需要考虑下面三种情况：

被移动的结点刚好就是尾结点，这种情况不需要做任何处理；
被移动的结点是头部结点；
被移动的结点在链表中间位置；

/** 把结点移动到链表尾部 */
public moveNodeToTail(node: LinkNode<K, V>) {
    /** 被移动的结点刚好就是尾结点，这种情况不需要做任何处理 */
    if (this.tail === node) return;

    /** 
     * 被移动的结点是头部结点时，
     * 当前结点要被移走，因此它的下一个结点将是头部结点，
     * 把头部结点指向它的下一个结点，同时设置头部结点的上一个节点为空（头部节点没有 lastNode）
     */
    if (this.head === node) {
        this.head = node.next;
        this.head.last = null;
    } 
    /**
     * 被移动的结点是中间结点时，
     * 该结点的上一个节点的 next 指针指向该结点的下一个结点
     * 该结点的下一个结点的 last 指针指向结点的上一个结点
     * 这样要被移动的结点就被“架空”了，没有指针再指向它
     */
    else {
        node.last.next = node.next;
        node.next.last = node.last;
    }

    /**
     * 最后是把要被移动的结点挂到链表尾部
     * 当前要被移动结点的上一个结点指向 tail 结点，next 将是空（因为它是尾结点了）
     * tail 结点的下一个结点指向当前要被移动的节点
     * 最后更新 tail 节点为要被移动的节点
     */
    node.last = this.tail;
    node.next = null;
    this.tail.next = node;
    this.tail = node;
}

最后是移除头部结点，这个方法主要是用于淘汰最少被使用的数据。

public removeHead() {
    if (!this.head) {
        return null;
    }

    /** 暂存头部节点 */
    const res = this.head;

    /** 如果链表中只有一个结点 */
    if (this.head === this.tail) {
        this.head = null;
        this.tail = null;
    } else {
        /**
         * 更新头部结点为它的下一个结点
         */
        this.head = res.next;
        res.next = null;
        this.head.last = null;
    }

    /** 返回头部结点 */
    return res;
}

LRU Cache 类

有了双向链表，接下来就是完成 LRU Cahce 类，用于实现LRU算法。

class LRUCache<K, V> {
    /** 缓存数据 */
    private keyNodeMap = new Map<K, LinkNode<K, V>>();

    /** 双向链表 */
    private doubleLinked = new DoubleLinkedList<K, V>();

    /**
     * @param capacity 缓存容量
    */
    constructor(private capacity: number) {}

    get(key: K) {}

    put(key: K, value: V) {}
}

首先是 get 方法，它内部判断传入的key在keyNodeMap是否可以找到，能找到就更新链表然后返回value即可。

get(key: K) {
    const node = this.keyNodeMap.get(key);

    if (!node) return null;

    /** 把结点移动到链表尾部 */
    this.doubleLinked.moveNodeToTail(node);
    
    return node.value;
}

最后是 put 方法，分两种情况：

如果是新增，则需要检查缓存是否已经满了，如果满了需要删除头节点然后再添加新结点；
如果是更新，与 get 操作类似，更新链表和 value 即可。

put(key: K, value: V) {
    const node = this.keyNodeMap.get(key);

    /** 更新 */
    if (node) {
        node.value = value;
        this.doubleLinked.moveNodeToTail(node);
    }
    /** 新增 */
    else {
        const newNode = new LinkNode(key, value);
        /** 
         * 首先判断有没有溢出，如果溢出了，
         * 则先删除头部结点，然后把新节点插入到尾部
        */
        if (this.keyNodeMap.size >= this.capacity) {
            const headNode = this.doubleLinked.removeHead();
            // 从 map 中也要移除
            this.keyNodeMap.delete(headNode.key);
        }

        this.keyNodeMap.set(key, newNode);
        this.doubleLinked.addNode(newNode);
    }
}

以上就是关于 LRU算法的全部代码，LRU算法用途广泛，在 Redis Key eviction 中，LRU算法被用于在内存中管理键值对的过期和淘汰。而 Vue 中的 KeepAlive 组件可以通过传入 max prop 来限制可被缓存的最大组件实例数，行为类似于LRU缓存：如果缓存的实例数量即将超过指定的那个最大数量，则最久没有被访问的缓存实例将被销毁，以便为新的实例腾出空间。

除了 LRU 算法外，还有 FIFO、LFU 等缓存置换算法。就不再展开了，大家感兴趣可以自行查阅资料深入了解。

原理​

算法实现​

实现双向链表​

LRU Cache 类​

原理

算法实现

实现双向链表

LRU Cache 类